Machine Learning 이론
공부하는 방식이 필요한 것을 찾다가 궁금한것이 있으면 그것을 공부하느라 이론이 주구난방식으로 되어 있을 수 있다. ( 추후 프로젝트 완료후 이론만 따로 정리하거나 그냥 냅두거나 해야겠다…)
Neural Networks
인공 신경망 모형은 neurons으로 구성된다. 각 뉴런은 input을 받아 weight에 곱하여 이를 모두 더한다. 이를 activation function(활성화 함수)를 거쳐 최종 output을 출력한다.
간단하게 이야기하면 여러개의 Input값들에 가중치인 Wn을 곱하여 Output을 찾아내는 방식.
여기서 Wn을 찾는 것이 궁극적인 목표.
수학식으로 표현하면 다음과 같다.
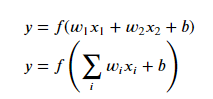
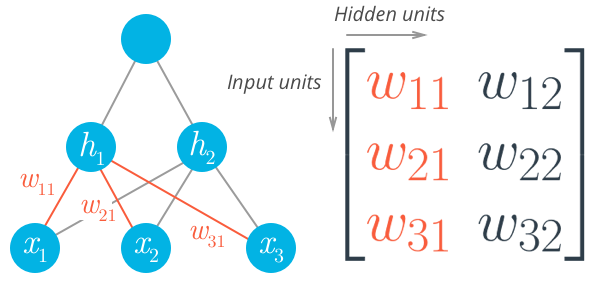
Input은 각 가중치를 곱한 값을 그다음 Layer에 전달한다. 즉 각각의 Layer에는 각각의 가중치가 있다는 것이다.
Activation Functions
- 일정 기준을 넘으면 이를 다른 뉴런에 전달하는 함수
- 입력신호의 총 합을 출력 신호로 변환하는 함수
가장 많이 사용되는 activation functions: Tanh (hyperbolic tangent), and ReLU (rectified linear unit).
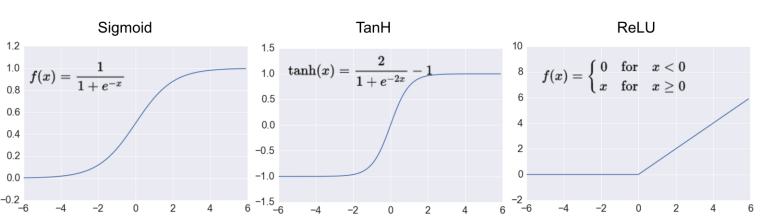
sigmoid
0~1사이의 확률 값을 출력한다. 생존/사망 또는 합격/불합격 처럼 class가 2개인 분류의 문제에 사용한다. sigmoid의 경우 입력층으로 갈수록 기울기가 작아지는 Gradient vanishing이 발생한다. Sigmoid의 경우 0~1 사이의 값이 나온다. 즉 소수점의 수들이 계속적으로 곱해지게 되면 0에 수렴하게 되는 것이다. 이렇게 될 경우 학습이 느려지고 제대로 되지 않는다.
Softmax
multi classification에 사용.
3개 이상의 class를 갖는 데이터에 대한 분류작업을 할때 사용한다. 총 class의 합이 1이 되는 확률이 나오게 된다.
RELU
- x>0x>0 이면 기울기가 1인 직선이고, x<0x<0이면 함수값이 0이된다.
- sigmoid, tanh 함수와 비교시 학습이 훨씬 빨라진다.
- 연산 비용이 크지않고, 구현이 매우 간단하다.
- x<0x<0인 값들에 대해서는 기울기가 0이기 때문에 뉴런이 죽을 수 있는 단점이 존재한다.
주로 ReLU function 이 hidden layers의 activation function으로 사용된다.
그 이유는 ReLU의 경우 Gradient vanishing 문제를 해결할 수 있다.
Loss Function - 손실함수
error, Loss : 모형의 예측값과 데이터의 실제값 간의 차이를 말한다.
즉 Test를 할때 실제 결과값과 예측값의 차이를 구하는 함수를 손실함수라고 한다.
MSE(Mean Squarred Error)
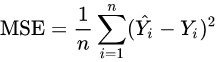
CEE(Cross Entropy Error)
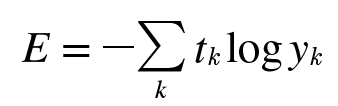
교차 엔트로피는 평균제곱오차와는 달리 오직 실제 정답과의 오차만을 파악하는 손실함수다.
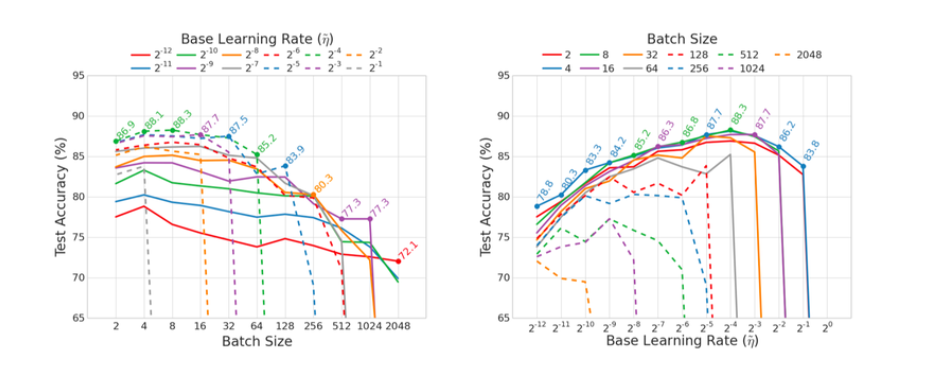
Batch_size
몇개의 Sample을 풀고 해답을 맞추는 지를 의미한다.
보통 32, 64를 선택한다. 이는 2의 제곱승이다.
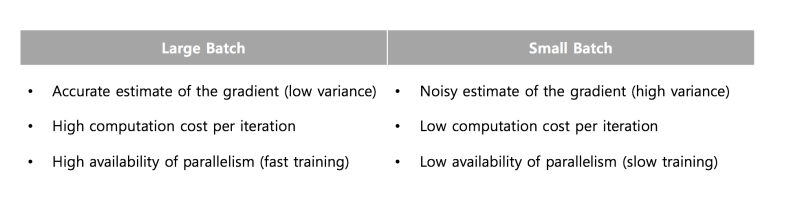
기본적으로 Batch사이즈가 작을경우 정확도가 증가하고 안정성이 높아진다. 그러나 너무 적은경우 오히려 더 부정확해진다